|
TigerJython | xx für Gymnasien |
Forum
Rekursionen
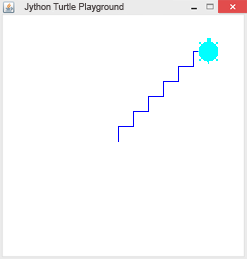
# Tu10.py from gturtle import * def step(): forward(20) right(90) forward(20) left(90) def staircase(n): if n == 0: return step() staircase(n-1) makeTurtle() staircase(6) |
|
Programmcode markieren
|
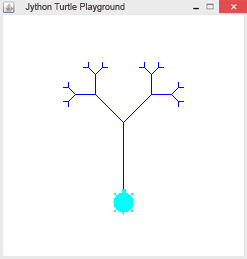
Beispiel 2: Der binäre Baum
|
|
Es ist wichtig, dass die Turtle nach dem Zeichnen des Baums an ihren Ursprünglich Position und Blickrichtung zurückkehrt.
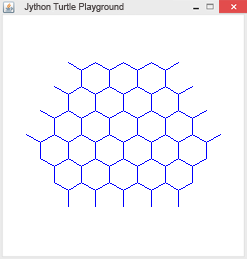
Beispiel 3: Wabenmuster
|
|
Beispiel 4: Quadratmuster
|

|
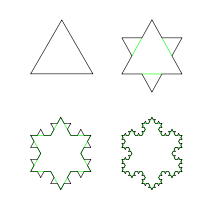
Beispiel 5: Koch-Kurve
|
|
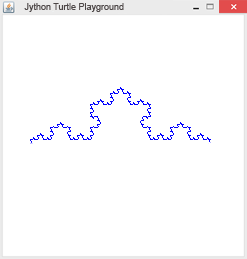
Beispiel 6: Peano
|

|
Beispiel 7: TreeFractal
|
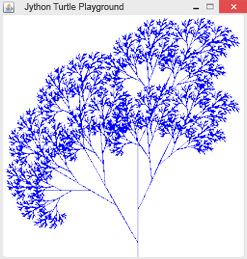
|
Beispiel 8: FlowerFractal
|

|
Beispiel 9: Sierpinsi Fraktal
|

|
| Aufgaben Serie 10 |
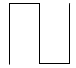
1) |
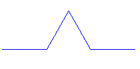
Erstelle die folgende Zeichnung mit Hilfe einer Rekursion. |
|
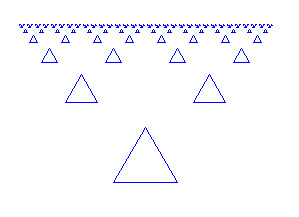 |
2) |
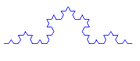
Erstelle die folgende Zeichnung mit Hilfe einer Rekursion. |
|
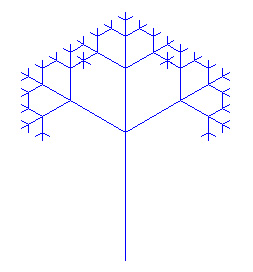 |
3) |
Ergänze den Programmcode so, dass eine Flocke gezeichnet wird. def figure(s):
|
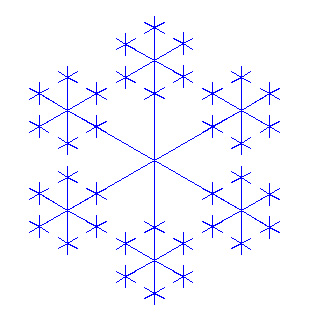 |
4) |
Ergänze die Kochkurve so, dass eine ganze Schneeflocke entsteht.
|
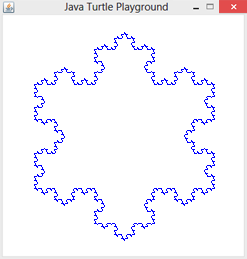 |
5) |
Die interessante Klothoide kann mit folgender rekursiven Funktion erstellt werden:
def clothoid(s):
if s > 1500:
Ergänze den Programmcode und teste die Rekursion für verschiedene Parameter s.
|
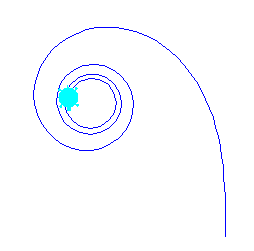 |