|
TigerJython | xx für Gymnasien |
Forum
Listen und Tupels
Statt Werte in verschiedenen Variable a, b, c einzeln abzuspeichern, stellt Python Listen und Tupels zur Verfügung, die als Behälter für beliebig viele Daten verwendet werden. Die Elemente einer Liste werden in eckigen Klammern zusammengefasst. In anderen Programmiersprachen verwendet man dazu oft Arrays. Im Gegensatz zu Arrays haben Listen keine feste, vordefinierte Länge, d.h. ihre Länge wird der Anzahl gespeicherter Elemente automatisch angepasst (dynamische Datenstruktur). Tupels werden mit runden Klammern zusammengefast und werden oft für die Koordinaten verwendet. |
|
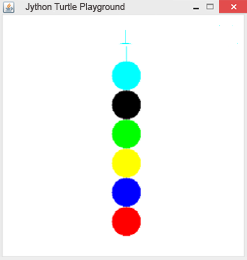
Beispiel 1: Liste mit Farben Die Liste colors enthält 6 Farben. Mit for c in colors: geht man die Liste durch, zeichnet mit jeder Farbe einen gefüllten Kreis und verschiebt die Turtle um 40 Schritte.
|
|
Erklärungen zum Programmcode:
| for c in colors : Die nachfolgende Anweisungen werden der Reihe nach für alle Elemente der Liste ausgeführt |
Beispiel 2: Elemente hinzufügen und auf einzelne Elemente zugreifen
|
Mit dem Befehl append kann eine Liste mit weiteren Elementen erweitert werden. ['red','blue','yellow','green','black','cyan','magenta'] Mit einem Index kann man auf die einzelnen Elemente der Liste zugreifen. Das erste Element hat den Index 0. colors[0] ist die Farbe red, colors[1] die Farbe blue usw.
|
|
Erklärungen zum Programmcode:
| colors.append("magenta") : fügt das Element "magenta am Ende der Liste colors hinzu | |
| print(colors): Zeigt alle Elemente der Liste | |
| print(colors[2]): Zeigt das Element mit dem Index 2 an, d.h. das dritte Element der Liste | |
| len(colors): Gibt die Anzahl Elemente (die Länge) der Liste an Weitere Befehle für den Umgang mit Liste sieht man unten auf dieser Website |
|
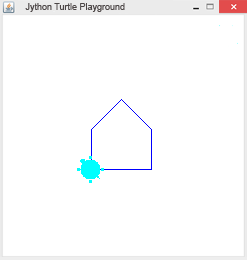
Beispiel 3: Liste mit Punkt-Koordinaten (Tupels) Die Liste house enthält die Koordinaten der Eckpunkte der neben stehenden Figur. Die Elemente der Liste sind Tupels (x, y). Im Programm geht man mit einer for-Schleife die Liste durch und verbindet die nacheinanderfolgende Punke. Auf die Elemente eines Tupels kann man gleich zugreifen, wie auf Elemente einer Liste. p[0] liefert das erste Element (x-Koordinate), p[1] liefert die y- Koordinate.
|
|
Erklärungen zum Programmcode:
| (0, 60) : Tupel mit Koordinaten eines Punktes | |
| house[2] : Das dritte Element der Liste house ist der Punkt p = (100, 60) | |
| print(p[0]) :Zeigt das erste Element des Tupels p an (die x-Koordinate 100) | |
| p[1] : Die y-Koordinate des Punktes p |
Beispiel 4: Elemente der Liste dynamisch per Mausklick hinzufügen
Die Anzahl Elemente einer Liste kann während der Programmausführung verändert werden. Es ist sogar möglich eine ganze Liste dynamisch zu erzeugen. Die Liste points ist zu Beginn leer. Mit jedem Mausklick wird ein Punkt mit den Koordinaten des Mausklicks erzeugt und gezeichnet.
|
 |
Erklärungen zum Programmcode:
| points= []: Erzeugt eine leere Liste | |
| p = (x, y): Koordinaten x, y des Mausklicks definieren den neuen Punkt p | |
| moveTo(q): Zeichnet eine Verbindungslinie vom Punkt p (aktuelle Mausposition) zum Punkt q. | |
| points.append(p): Fügt den Punkt p zu der Liste points | |
| print(points): Zeigt die aktuelle Liste im Ausgabenfenster |
Beispiel 5: Linke Maustaste erzeugt Punkte, rechte Maustaste erzeugt ein gefülltes Polygon
Die Ecken des Polygon werden per linken Mausklick erzeugt. Die Liste corner ist zu Beginn leer. Mit jedem Mausklick wird ein Punkt hinzugefügt und aktuelle Punktezahl angezeigt. Ein Klick mit der rechten Maustaste beendet die Punkterzeugung. in einer for-Schleife werden alle Punkte der Reihe nach zu einem Polygon verbunden und die Polygonfläche rot gefüllt.
|
|
Erklärungen zum Programmcode:
| corner = []: Erzeugt eine leere Liste | |
| corner.append(p): Fügt den Punkt p zur Liste corner hinzu | |
| print(len(corner)): Anzahl Elemente der Liste (Länge der Liste) wird angezeigt | |
| for q in corner:: Geht die Liste aller Punke durch |
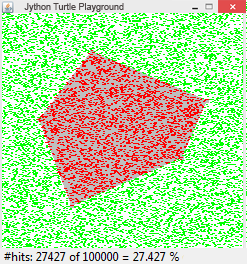
Beispiel 6: Fläche eines Polygons mit Monte Carlo-Methode bestimmen
|
Mit der Funktion getPixelColorStr() kann man herausfinden, ob die Farbe unter einem zufällig gewählten Punkt weiss oder grau ist. Die Tropfen in der grauen Fläche werden als Hits gezählt und rot markiert, die übrigen grün. Da es vorkommen kann, dass ein Punkt mehrmals getroffen wird, müssen bei den Treffern auch die bereits rot gefärbten Punkte als Hits gezählt werden.
|
|
Aus dem Verhältnis der Anzahl Treffer zu Anzahl aller Punkte, die man auf das Turtlefenster fallen lässt, lässt sich die Polygonfläche berechnen. Eine höhere Genauigkeit erreicht man, wenn man die Anzahl der Zufallspunkte erhöht. Das Ergebnis wird in der Statuszeile angezeigt. Wenn d ie Funktion startRandomRain() im Callback der rechten Maustaste aufgerufen wird, erscheinen die Zufallspunkte alle gleichzeitig nach dem alle 100 000 Zufallstropfen gelandet sind. Unter verwendung von putSleep() und wakeUp() werden die Zufallstropfen "animiert" eins nach dem anderen dargestellt. Der Befehl startRundomRain() wird im Hauptprogramm mit putSleep() angehalten und gestartet, nach dem im Callback der rechten Maustaste wakeUp() aufgerufen wurde. Testen Sie den Unterschied, indem Sie startRandomRain() im Callback aktivieren und die wakeUp() und die letzten zwei Zeilen im Hauptprogramm deaktivieren. |
# Tu13e.py from gturtle import * import random def onMousePressed(x, y): if isLeftMouseButton(): p = (x, y) setPos(p) dot(5) corner.append(p) if isRightMouseButton(): setFillColor("gray") startPath() for q in corner: moveTo(q) fillPath() #startRandomRain() wakeUp() def startRandomRain(): nbHit = 0 for i in range(n): p = (random.randint (-300, 300), random.randint (-300, 300)) setPos(p) color = getPixelColorStr() if color == "white": setPenColor("green") dot(2) if color == "gray" or color == "red": nbHit += 1 setPenColor("red") dot(2) setStatusText("#hits: " + str(nbHit) + " of " + str(n) + " = " + str(nbHit/n * 100) + " % of windowarea") makeTurtle(mousePressed = onMousePressed) addStatusBar(20) setStatusText("Left click to select corners, right click to start dropping") setPenColor("gray") hideTurtle() corner=[] n = 100000 putSleep() startRandomRain() |
| Programmcode markieren
|
Erklärungen zum Programmcode:
| startRandomRain(): Erzeugung n Zufallspunkte | |
| getPixelColorStr(): gibt die Hintergrundfarbe an der Turtleposition zurück | |
| putSleep(): Hält den Programmablauf an, bis wakeUp() aufgerufen wird | |
| wakeUp(): Führt angehaltenen Programmablauf weiter |
Beispiel 6: Regenbogenfarben aus einer Farbenliste auswählen
Der Befehl X11Color.RAINBOW_COLORS() liefert eine Liste mit 40 Farben. Diese wird als Liste colors gespeichert. Mit einer for-Schleife geht man diese Liste duch und zeichnet jeweils eine senkrechte Linie mit der Breite 10 Pixel.
|
 |
Erklärungen zum Programmcode:
| colors = X11Color.RAINBOW_COLORS() : Liste mit 40 Regenbogenfarben | |
| colors[i] : Das i-te Element der Liste | |
| setPenWidth(10) bewirkt, dass die gezeichneten linien 10 Pixel breit sind |
| Aufgaben Serie 13 |
1. |
|
 |
|
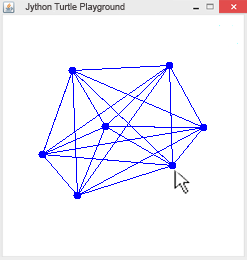
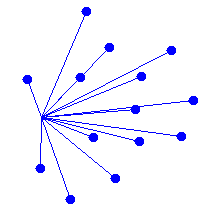
| 2. | Mit dem linken Mausklick werden beliebig viele Punkte gezeichnet und in einer Liste gespeichert. Klickt man mit der rechten Maustaste, so werden vom Punkt des Mausklicks aus Verbindungslinien zu allen gespeicherten Punkten gezeichnet.
|
 |
|
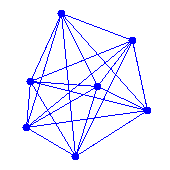
| 3. | Im Beispiel 4 wird die Liste points per Mausklick mit neuen Punkten ergänzt und jeder neue Punkt mit allen Punkten der Liste verbunden. Ergänze das Programm so dass bei jedem Mausklick auch die Anzahl der Verbindungslinien gezänlt wird. Die Zählervariable n wird im Hauprogramm mit n = 0 initialisiert beim Zeichnen jeder Verbindungslinie um 1 erhöht. def onMousePressed(x, y): global n p = (x, y) setPos(p) ...... Vergleiche das Ergenbis mit der kombinatirischen Formel n * (n - 1) / 2. |
 |
|
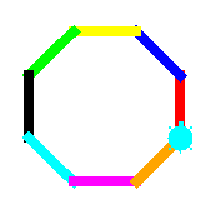
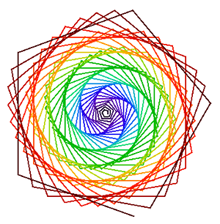
| 4. | Erstelle eine Liste colors mit 8 Farben. Definiere eine Funktion line(color, length), der eine farbige Linie zeichnet. Zeichnen Sie eine Spirale, so wie im Bild rechts. Nach jeder gezeichneten Strecke wird die nächste Farbe aus der Liste colors genommen. Nach dem man die letzte farbe genommen hat, beginnt man wieder mit der ersten Farbe.
|
 |
|
| 5. | colors = X11Color.RAINBOW_COLORS
|
 |
Zusatzstoff: Sortieralgorithmen
Sortieralgorithmen gehören zu den wichtigsten und meist verwendeten Verfahren der Informatik. Obwohl in vielen Programmiersprachen, so auch in Python, vordefinierte Sortierfunktionen existieren, gehören die Konzepte des Sortierens zum Standardwissen, denn es gibt immer wieder Situationen, in welchen man das Sortieren selbst implementieren muss.
Beispiel 6: Eine Liste mit n Elementen mit BubbleSort der Grösse nach ordnen
Die Sortierung mit BubbleSort-Algorithmus erfolgt wie folgt:
- Man geht die Liste vom ersten bis zum vorletztem Element durch und vergleicht jedes Element mit dem nachfolgendem
- Ist das Element grösser als sein Nachfolger, wird die Reihenfolge der beiden Elementen vertauscht
- Das grösste Element steht danach am Ende der Liste
- Man wiederholt den Vorgang mit den übrigen n - 1 Elementen und plaziert das zweitgrösste Element an die vorletzte Position. Dann wiederholt man dasselbe mit den restlichen n-2 Elementen, n-3 Elementen usw.
# BubleSort1.py def bubbleSort(li): n = len(li) for i in range(n - 1, 0, -1): for k in range(i): if li[k] > li[k + 1]: li[k + 1],li[k] = li[k],li[k + 1] li = [85, 34, 57, 13, 25, 39, 44, 7, 68, 30] bubbleSort(li) print(li) |
| Programmcode markieren
|
Ergebnis:
[7, 13, 25, 30, 34, 39, 44, 57, 68, 85]
Erklärungen zum Programmcode:
| len(li): Anzahl Elemente der Liste li | |
| for i in range(n - 1, 0, -1): Zuerst die ersten n-1 Elemente durchgehen, dann die ersten n-2 Element, n-3 Elementen usw. | |
| li[k + 1], li[k] = li[k], li[k + 1]): Vertauscht die Reihenfolge der zwei Elemente der Liste li |
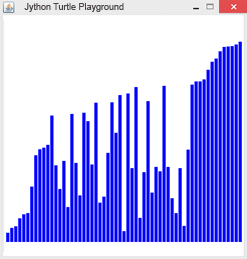
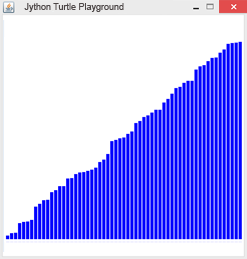
Beispiel 7: Grafische Darstellung des BubbleSort-Algorithmus n zufällig gewählte Zahlen zwischen 1 und 500 werden mit dem BubbleSort-Algorithmus sortiert. Um den Sortiervorgang grafisch darzustellen, zeichnet man für jede Zahl einen Balken, dessen Höhe in Pixel der Zufallszahl entspricht. Danach wird die Liste sortiert und die Balken nach jedem Sortierungsschritt neu dargestellt. Die Funktion drawBar(s) zeichnet einen Balken der Länge s.
|
|
# BubbleSort2.py from gturtle import * from random import randint d = 10 n = 59 def createRandomBars(): for i in range(n): s = randint(1, 500) li.append(s) drawAllBars() def drawBar(s): left(90) penDown() forward(s) back(s) penUp() right(90) def drawAllBars(): clear() setPos(-290, -250) for s in li: drawBar(s) forward(d) def bubbleSort(): for i in range(n-1, 0, -1): for k in range(0, i): if li[k] > li[k + 1]: li[k + 1],li[k] = li[k],li[k + 1] drawAllBars() repaint() Turtle.sleep(10) makeTurtle() enableRepaint(False) ht() right(90) setPenWidth(8) li = [] createRandomBars() bubbleSort() |
| Programmcode markieren
|
Erklärungen zum Programmcode:
| enableRepaint(False): verhindert das automatische Rendern | |
| repaint(): stellt die ganze Grafik auf dem Bildschirm dar | |
| Turtle.sleep(10): damit man das Sortieren bessert verfolgen kann, wird das Programm nach jedem Sortierdurchgang 10 ms angehalten |
Beispiel 8: n Farbkugeln mit BubbleSort nach Regebogen-Spektrum sortieren
|
# BubbleSort3.py from gturtle import * from random import randint d = 15 n = 41 def createRandomDots(): for i in range(n): c = makeColor("rainbow", randint(10, 90) / 100) li.append(c) drawAllDots() def drawAllDots(): setPos(-295, 0) for c in li: setPenColor(c) dot(d - 1) forward(d) def getHsb(c): hsb = Color.RGBtoHSB(c.getRed(), c.getGreen(), c.getBlue(), [0, 0, 0]) return hsb[0] def bubbleSort(): for i in range(n - 1, 0, -1): for k in range(i): if getHsb(li[k]) > getHsb(li[k + 1]): li[k + 1],li[k] = li[k],li[k + 1] drawAllDots() repaint() Turtle.sleep(10) makeTurtle() clear("black") enableRepaint(False) right(90) li = [] createRandomDots() bubbleSort() |
| Programmcode markieren
|
Erklärungen zum Programmcode:
| makeColor("rainbow", randint(10, 90) / 100): erzeugt eine zufällige Regenbogenfarbe | |
| RGBtoHSB(): konvertiert eine RGB-Farbe zu | |
| Turtle.sleep(10): damit man das Sortieren bessert verfolgen kann, wird das Programm nach jedem Sortierdurchgang 10 ms angehalten |
Beispiel 9: QuickSort-Algorithmus Der BubbleSort-Algorithmus ist einfach nachvollziehbar, ist aber nicht so effizient. In der Praxis werden deshalb effizientere Sortierverfahren verwendet, wie z.Bsp. QuickSort. Der Programmcode ist einiges komplizierter als bei BubbleSort und wird an dieser Stelle nur als Demonstration aufgeführt, damit man die die Geschwindigkeit beider Sortierverfahren vergleichen kann. Eine Beschreibung des Algorithmus findet man beispielsweise auf Wikipedia. [https://de.wikipedia.org/wiki/Quicksort]
|
|
# QuickSort.py from gturtle import * from random import randint d = 10 n = 59 def createRandomBars(): for i in range(n): s = randint(1, 500) li.append(s) drawAllBars(li) def drawBar(s): left(90) penDown() forward(s) back(s) penUp() right(90) def drawAllBars(li): clear() setPos(-290, -250) for s in li: drawBar(s) forward(d) def quickSort(li): quickSortHelper(li,0,len(li)-1) def quickSortHelper(li,first,last): if first<last: splitpoint = partition(li,first,last) quickSortHelper(li,first,splitpoint-1) quickSortHelper(li,splitpoint+1,last) def partition(li,first,last): pivotvalue = li[first] leftmark = first+1 rightmark = last done = False while not done: while leftmark <= rightmark and li[leftmark] <= pivotvalue: leftmark = leftmark + 1 while li[rightmark] >= pivotvalue and rightmark >= leftmark: rightmark = rightmark -1 if rightmark < leftmark: done = True else: temp = li[leftmark] li[leftmark] = li[rightmark] li[rightmark] = temp temp = li[first] li[first] = li[rightmark] li[rightmark] = temp drawAllBars(li) repaint() Turtle.sleep(10) return rightmark makeTurtle() enableRepaint(False) ht() right(90) setPenWidth(8) li = [] createRandomBars() quickSort(li) |
| Programmcode markieren
|
| Aufgaben |
| 6. | In Python gibt es eine eingebaute Funktion sort(). |
| 7. | colors = X11Color.RAINBOW_COLORS from gturtle import * makeTurtle() hideTurtle() s = 5 repeat 200: forward(s) left(70) s = s + 1 Du gehst die Liste colors durch und zeichnest jeweils 5 Strecken mit der gleichen Farbe. |
 |
colors1 = list(reversed(colors)) |
 |
Die wichtigsten Operationen mit Listen
li = [1, 2, 3, 4] li = [1, "a", [7 , 5]] li[i] li[start:end] li[start:end:step] li[start:] li[:end] li.append(element) li.insert(i, element) li.extend(li2) li.index(element) li.pop(i) pop() li1 + li2 li1 += li2 li * 4 [0] * 4 len(li) del li[i] del li[start:end] del li[:] list(reversed(li)) li.sort() x in li x not in li li[k+1], li[k] = li[k], li[k+1] |
Liste mit den Zahlen 1, 2, 3, 4 definieren Liste mit unterschiedlichen Datentypen definieren Auf Listenelement mit Index i zugreifen Neue Teilliste mit Elementen start bis end, aber ohne end Neue Teilliste mit Elementen start bis end mit Schritt step Neue Teilliste mit allen Elementen von start an Neue Teilliste von ersten Element bis end, aber ohne end Anfügen ans Ende Einfügen an Stelle i (Element i rutscht nach rechts) Elemente aus li2 anfügen (Konkatenation) Sucht das erste Vorkommen und gibt dessen Index zurück Entfernt das Element mit Index i und gibt es zuück Entfernt das letzte Element und gibt es zurück Gibt die Konkatenation von li1 und li2 in neuer Liste zurück Ersetzt li1 durch die Konkatenation von li1 und li2 Neue Liste mit Elementen von li viermal wiederholt Neue Liste mit der Länge 4 (jedes Element Zahl 0) Gibt die Anzahl Listenelemente zurück Entfernt das Element mit Index i Entfernt alle Elemente von start bis end, aber ohne end Entfernt alle Elemente, es bleibt eine leere Liste Kehrt die Liste li um (letztes Element wird das erste) Sortiert die Liste (Vergleich mit Standardverfahren) Gibt True zurück, falls x in der Liste enthalten ist Gibt True zurück, falls x nicht in der Liste enthalten ist Vertauscht die Reihenfolge zwei nacheinanderfolgenden Elemente |